20 sliding algorithms
None of the methods learned before seem appropriate to deal with non-stationary data. A simple solution is to apply those methods for sliding windows of “appropriate” widths.
20.1 Sliding Z-score
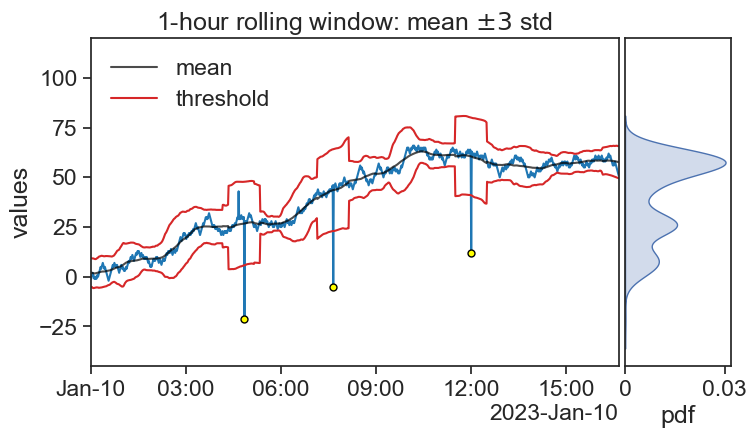
Now the Z-score seems to give really nice results (but not perfect). Maybe playing with the window width and Z-score threshold would give better results?
In any case, we clearly see why the Z-score is not a robust algorithm. See how the standard deviation is sensitive to outliers?
20.2 Sliding IQR
Let’s see how well the sliding IQR method fares.
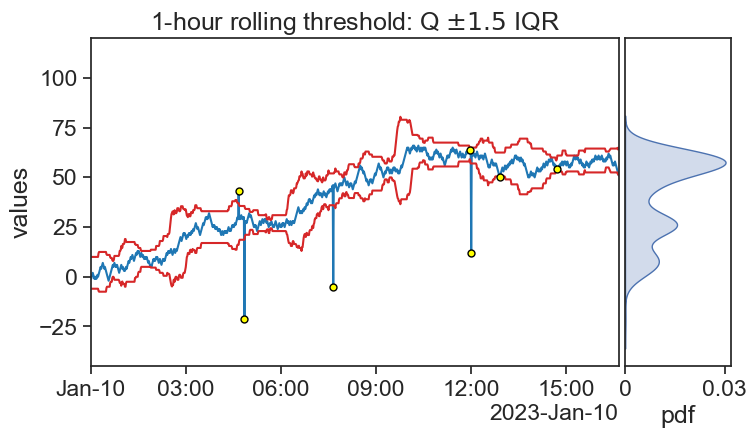
It identified all the outliers, but also found that a few other points should be considered outliers? What do you think of that?
See that the threshold does not jump abruptly when the sliding window includes an outlier. In fact, the threshold doesn’t even care! This is what it means to be robust.
However, we do see large fluctuations in the threshold. When does this happen? Why?
20.3 Sliding MAD
Now it’s MAD’s time to shine.
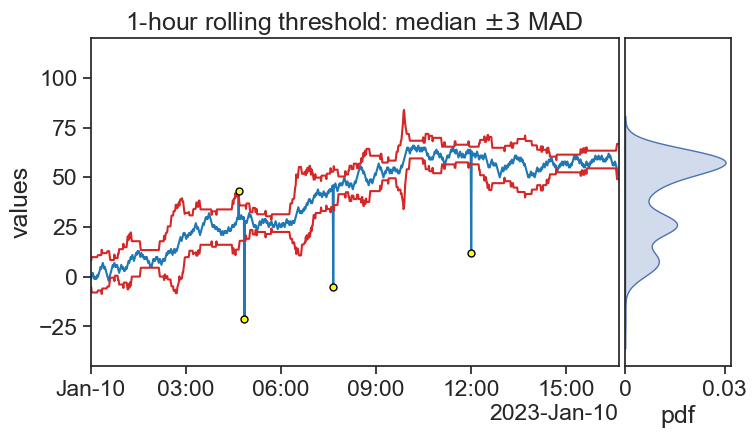
Compare this result to the previous two. Which yields best results?
MAD is robust to outliers, and again we see that the threshold envelope widens when there is a rising or falling trend in the data.
20.4 Challenges
Now it’s your turn to work, I’m tired! Write algorithms for the following outlier identification methods:
- visual inspection
- Z-score
- IQR
- MAD
Excluding the visual inspection method, write first an algorithm that operates on a full time series, and then write a new version that can work with sliding windows.
