19  robust analysis

A tool is said to be robust if outliers don’t influence (much) its results.

The average and standard deviation are not robust.

import numpy as np
series1 = np.array([0, 1, 2, 3, 4, 5, 6])
series2 = np.array([0, 1, 2, 3, 4, 5, 60])
print(f"series 1: mean={series1.mean():.2f}, std={series1.std():.2f}")
print(f"series 2: mean={series2.mean():.2f}, std={series2.std():.2f}")

series 1: mean=3.00, std=2.00
series 2: mean=10.71, std=20.18

On the other hand, the median and IQR are robust:

from scipy.stats import iqr
print(f"series 1: median={np.median(series1):.2f}, IQR={iqr(series1):.2f}")
print(f"series 2: median={np.median(series2):.2f}, IQR={iqr(series2):.2f}")

series 1: median=3.00, IQR=3.00
series 2: median=3.00, IQR=3.00

19.1 MAD

Another rubust method is MAD, the Median Absolute Deviation, given by

$$\text{MAD} = \text{median}(\left| x_i - \text{median}(x) \right|),$$

where $|\cdot|$ is the absolute value.

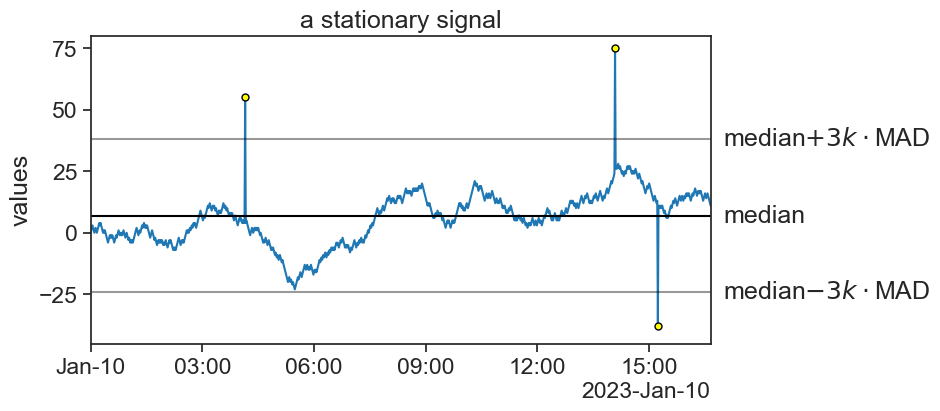
Applying MAD to the stationary time series from before, yields

Here, the threshold is the median $\pm3k\cdot$ MAD, where the value $k=1.4826$ scales MAD so that when the data is gaussianly distributed, $3k$ equals 1 standard deviation.