49  practice 2

In this practice we will find the frequency of an interesting oscillation in transpiration measured from a grapevine leaf using a LICOR 6400. We thank Yotam Zait for providing us this interesting measurement.

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import scipy
import seaborn as sns
sns.set(style="ticks", font_scale=1.1)
pd.set_option('mode.chained_assignment', None)
# %matplotlib widget

df = pd.read_csv("grapevine_E.csv",
                 index_col='date', parse_dates=True)
df

	E
date
2023-07-10 10:37:30	0.004116
2023-07-10 10:38:30	0.004012
2023-07-10 10:39:30	0.003694
2023-07-10 10:40:30	0.003506
2023-07-10 10:41:30	0.003361
...	...
2023-07-13 20:14:23	0.000059
2023-07-13 20:15:23	0.000069
2023-07-13 20:16:23	0.000061
2023-07-13 20:17:23	0.000063
2023-07-13 20:18:23	0.000061

4886 rows × 1 columns

start = '2023-07-12'
end = '2023-07-13'
df = df[start:end]

fig, ax = plt.subplots()
df['E'].loc[df['E']<4.5e-5] = np.nan
df['E'].ffill(inplace=True)
df['E'].plot()
ax.set(ylabel="transpiration")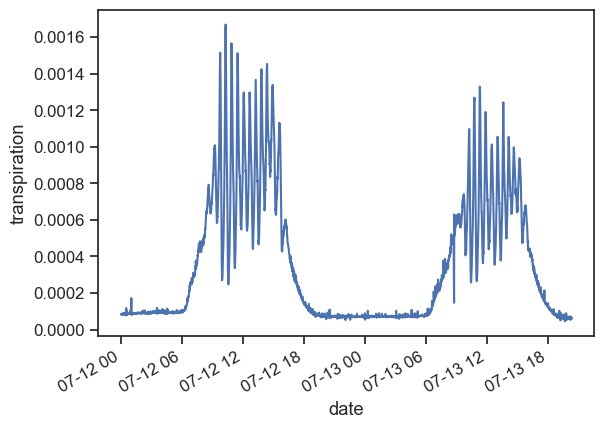

The measurements shown above suggest that there is a clear oscillatory pattern in the grapevine transpiration. Zooming in, we see that the oscillation period is about once every half hour. Let’s find out exactly what the period is.

N = len(df)
F = scipy.fft.fft(df['E'].values) / N
n = np.arange(N)
# the basic time unit here is "second"
# measurements every 60 seconds
dt = 60  # seconds
freq = scipy.fft.fftfreq(N, d=dt)

# Get the one-sided spectrum
n_oneside = N//2
# get the one side frequency
k_oneside = freq[:n_oneside]
F_oneside = F[:n_oneside]
fig, ax = plt.subplots()
ax.plot(k_oneside, np.abs(F_oneside))
ax.set(xlabel='freq (Hz)',
       ylabel='|F(freq)|')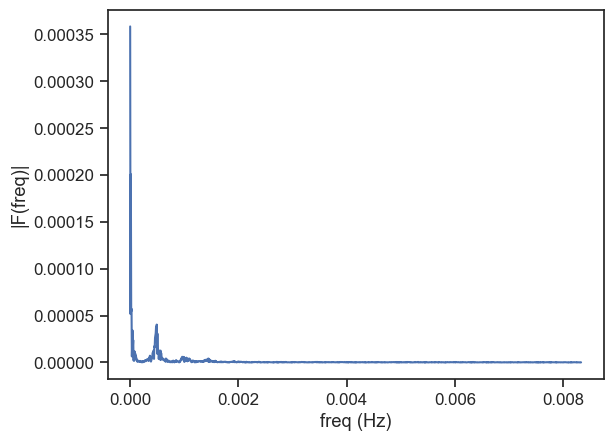

The first peak corresponds to very low frequencies (day), and the second peak is probably what we need. Let’s focus on that.

# ignore periods longer then 120 min
cutoff = 1 / (120*60)
mask = np.where(k_oneside > cutoff)
k_oneside = k_oneside[mask]
F_oneside = F_oneside[mask]

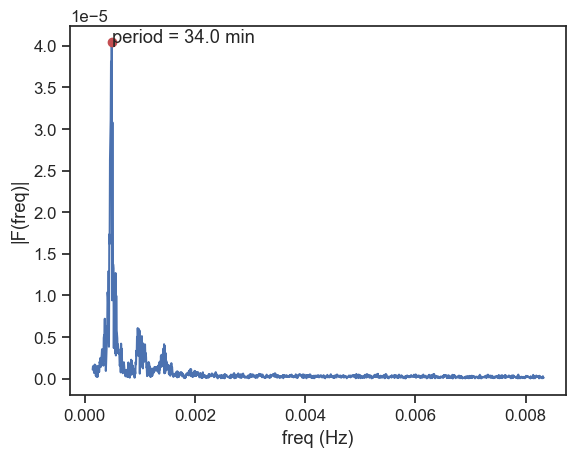
index_max = np.argmax(np.abs(F_oneside))
k_max = k_oneside[index_max]
F_max = np.abs(F_oneside[index_max])
period = 1 / k_max

fig, ax = plt.subplots()
ax.plot(k_oneside, np.abs(F_oneside))
ax.plot([k_max], [F_max], 'ro')
ax.text(k_max, F_max, f"period = {period / 60:.1f} min")
ax.set(xlabel='freq (Hz)',
       ylabel='|F(freq)|')