Book 1, Proposition 02
Make a line segment of the same length of another, starting from a given point.

Proposition 2, Problem
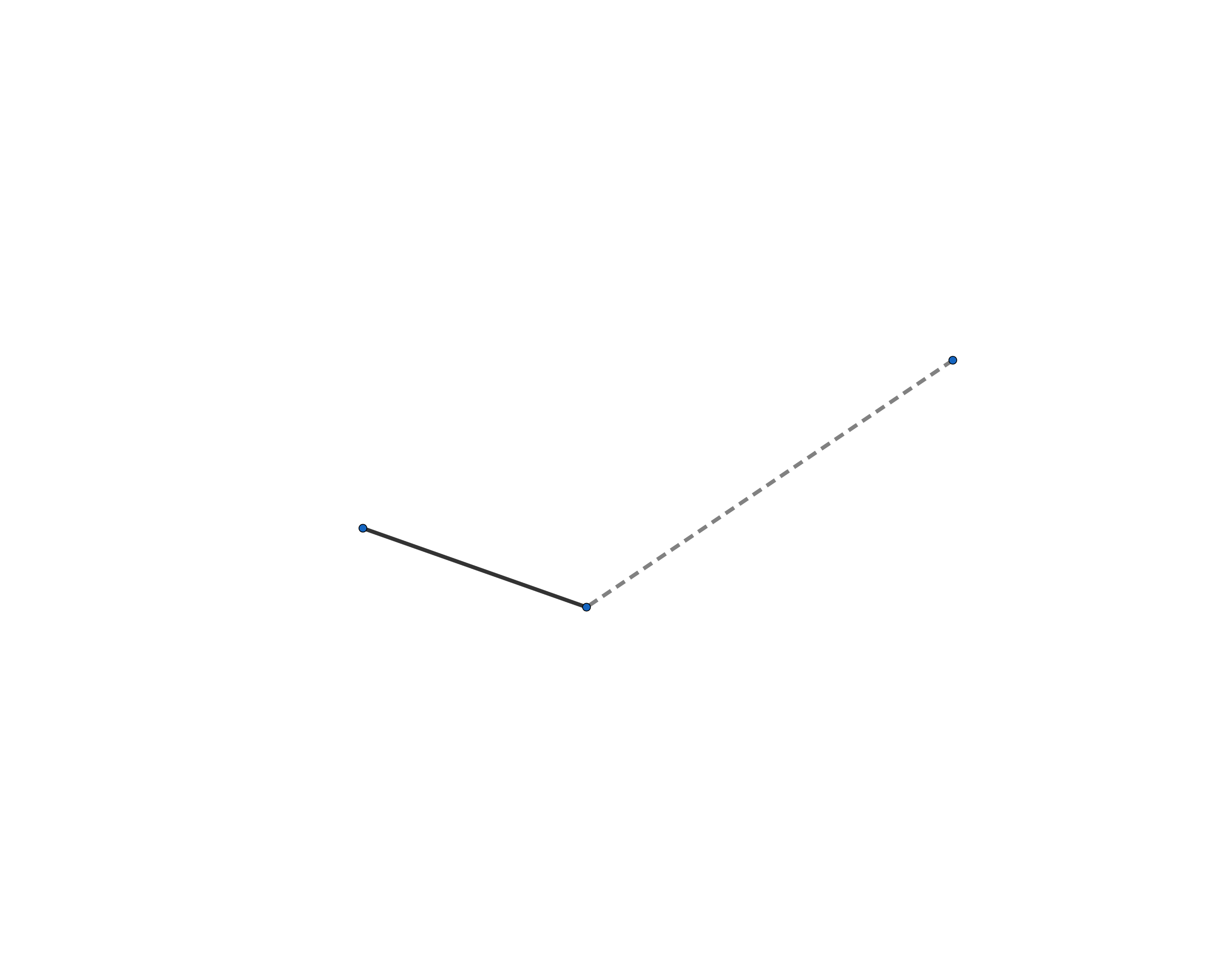
From a given point to draw a straight line equal to a given finite straight line.

Draw the dashed line $( {\color{#000} \rule[-0.5em]{0.2cm}{2pt} } {\color{#FFF} \rule[-0.5em]{0.2cm}{2pt} } {\color{#000} \rule[-0.5em]{0.2cm}{2pt} } {\color{#FFF} \rule[-0.5em]{0.2cm}{2pt} } {\color{#000} \rule[-0.5em]{0.2cm}{2pt} } )$, (post. 1.)
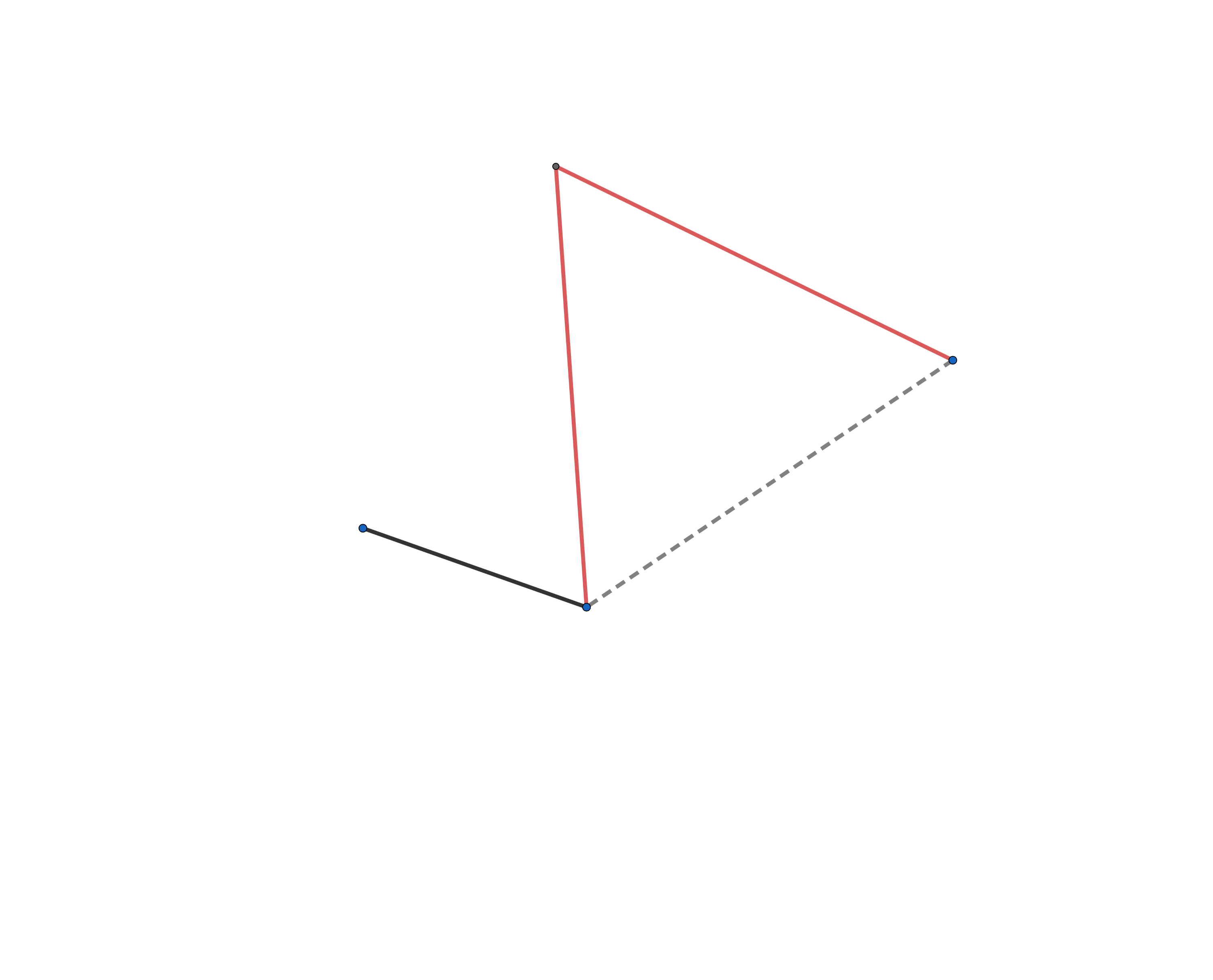
Describe the equilateral triangle (red-red-dashed) (prop. 1), produce red line $({\color{#D32F2F} \rule[-0.5em]{1cm}{2pt} })$ on the left (post. 2.).
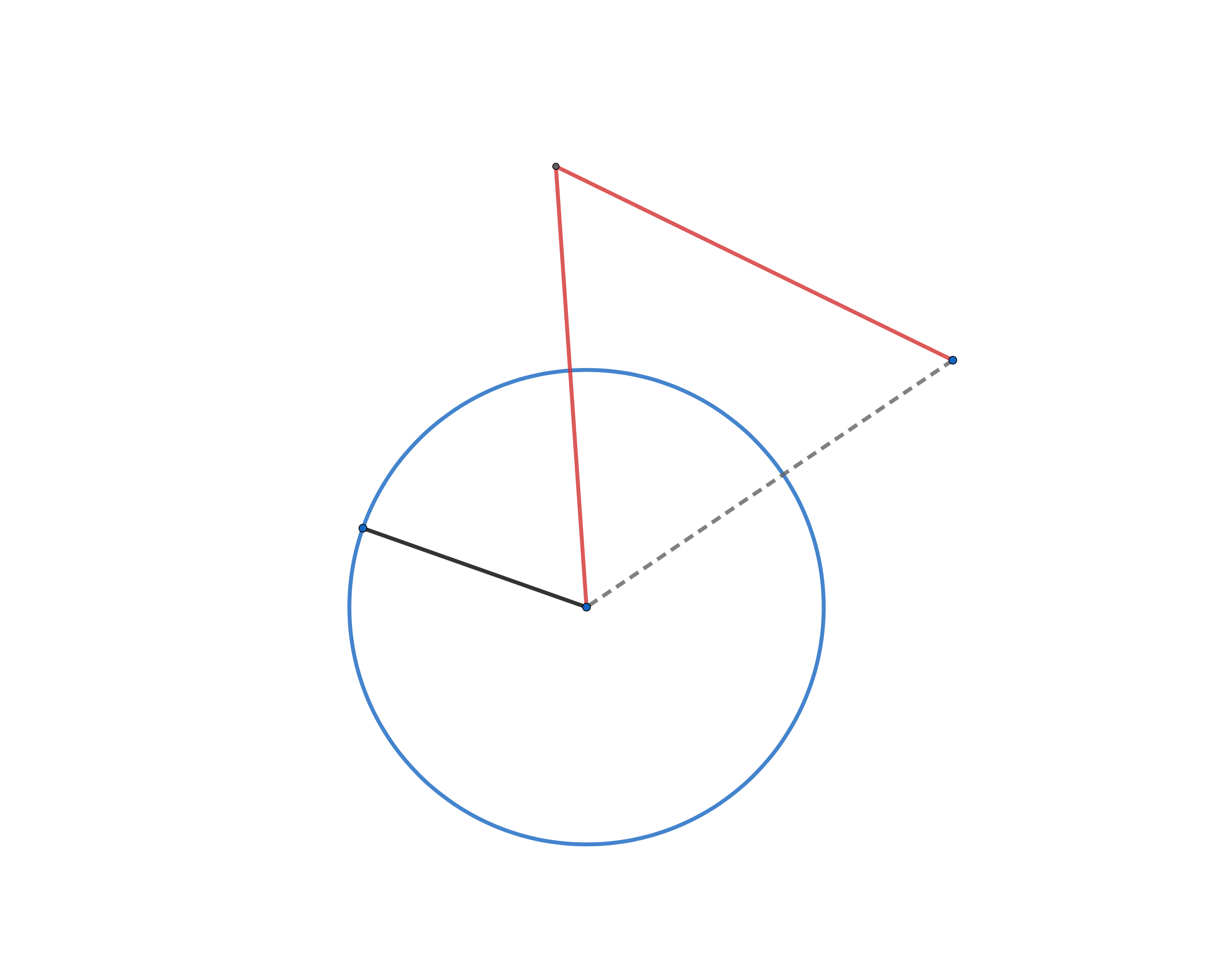
Describe the blue circle, whose radius is the black line $({\color{#000} \rule[-0.5em]{1cm}{2pt} })$ (post. 3.).
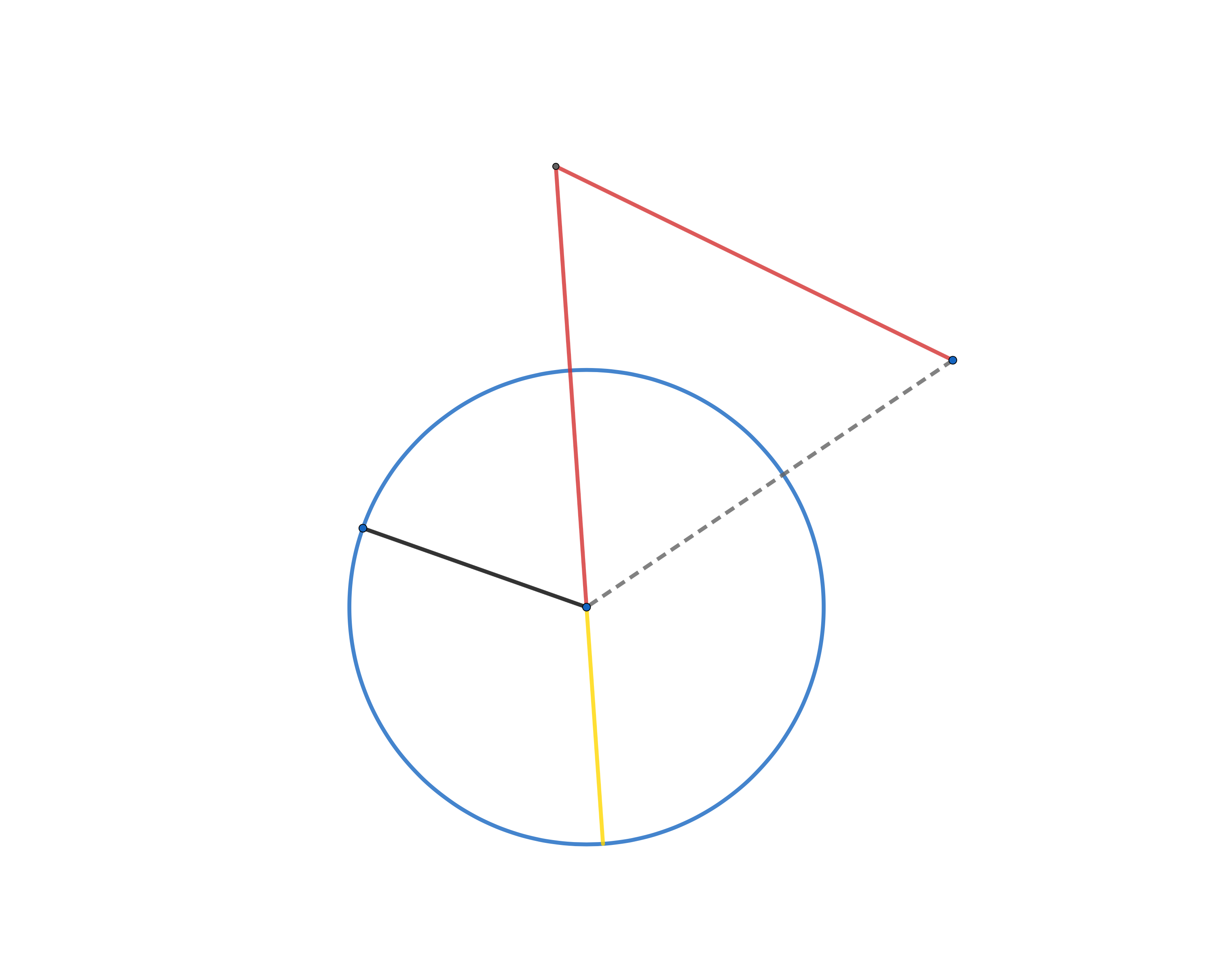
Construct the yellow line $({\color{#FFd700} \rule[-0.5em]{1cm}{2pt} })$, continuation of left red line $({\color{#D32F2F} \rule[-0.5em]{1cm}{2pt} })$, until it reaches the blue circle.
Construct the red circle (post. 3.), whose radius is the red-yellow line $( {\color{#D32F2F} \rule[-0.5em]{0.5cm}{2pt} } {\color{#FFd700} \rule[-0.5em]{0.5cm}{2pt} } )$ .
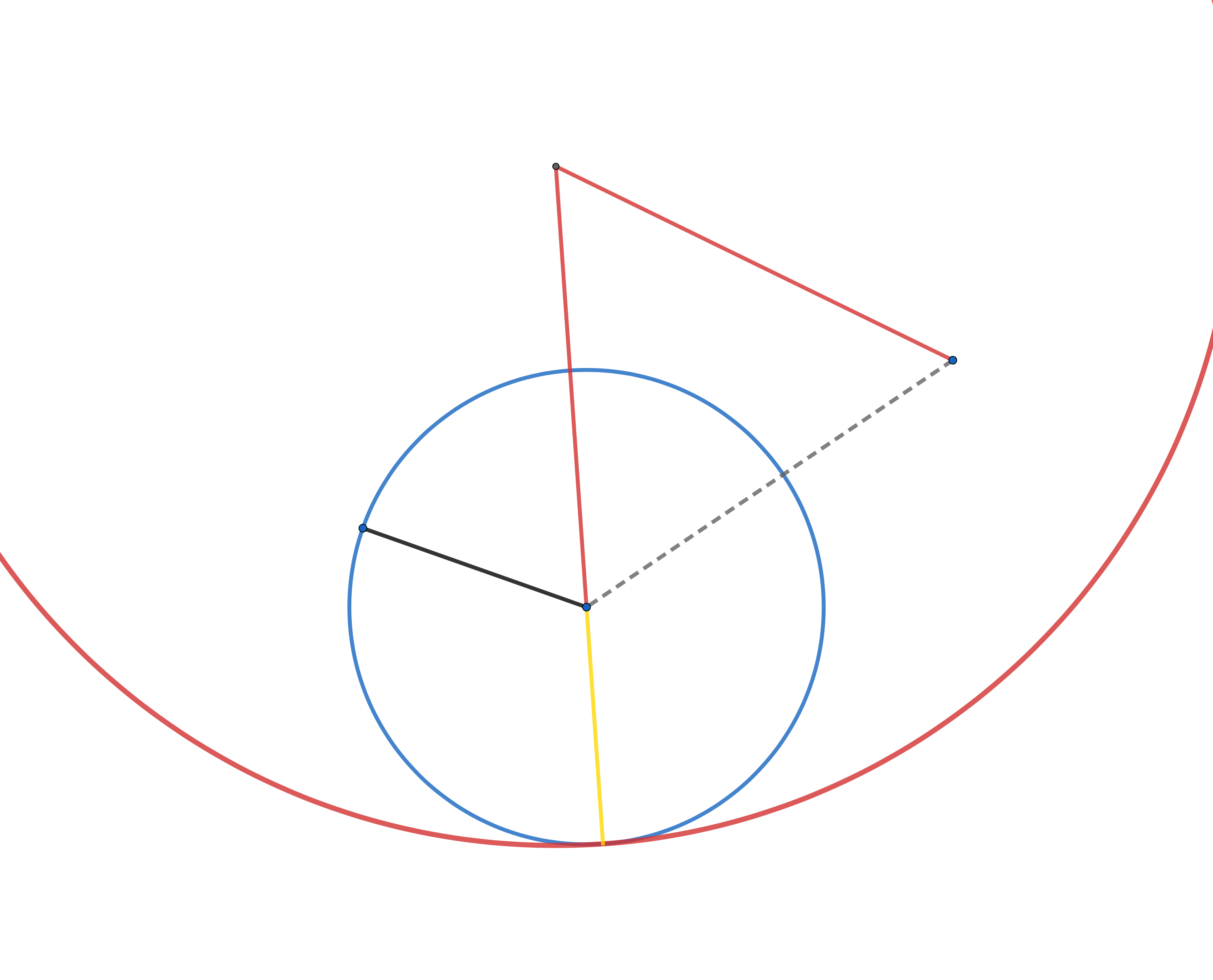
Construct the blue line $({\color{#1565C0} \rule[-0.5em]{1cm}{2pt} })$, (post. 2.), which is the continuation of the right red line $({\color{#D32F2F} \rule[-0.5em]{1cm}{2pt} })$ , until it reaches the red circle.
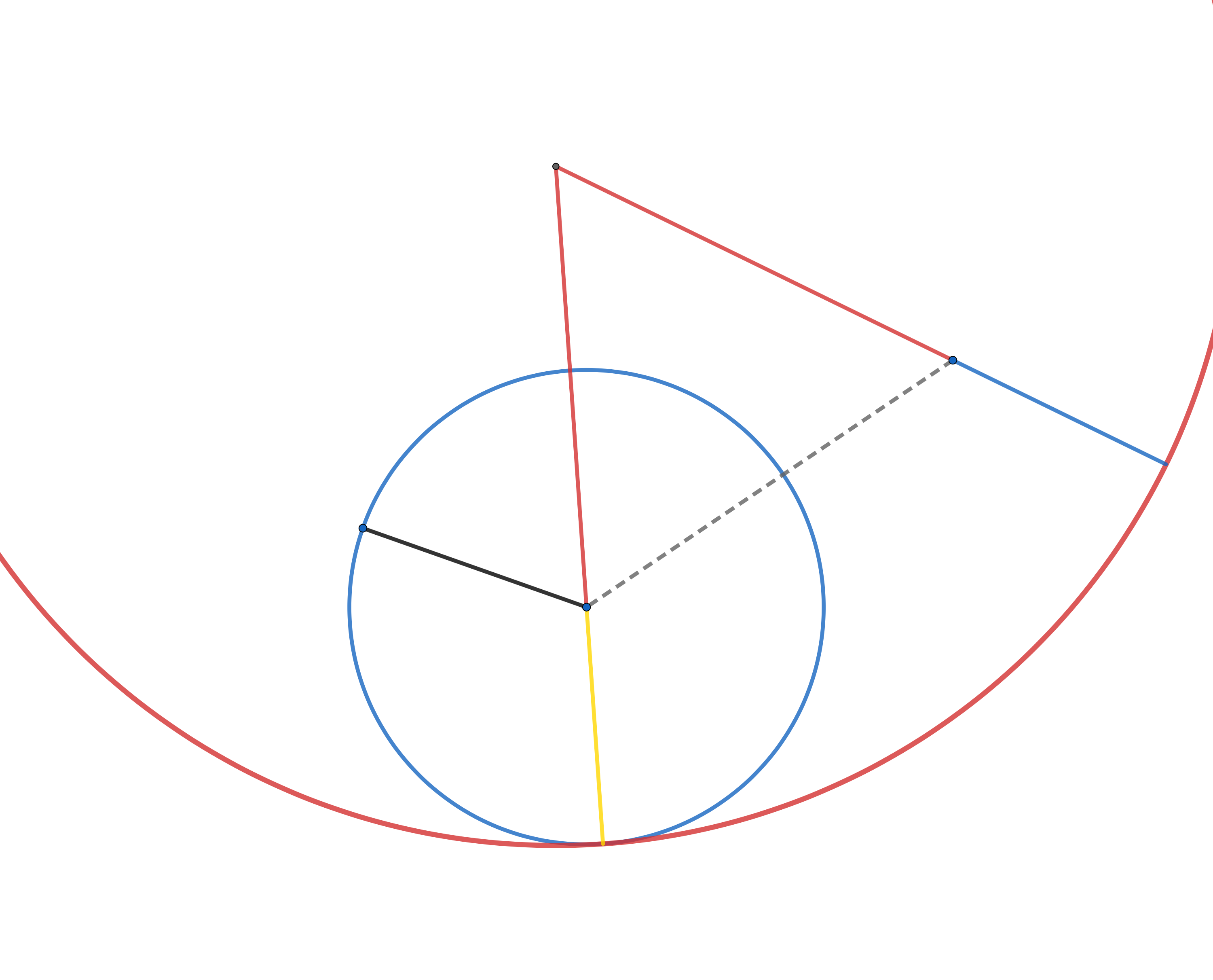
The blue line $({\color{#1565C0} \rule[-0.5em]{1cm}{2pt} })$ is the required line.
For
(def. 15.), and
(const.),
(ax. 3.), but (def. 15.)
therefore ${\color{#1565C0} \rule[-0.5em]{1cm}{2pt} }$ drawn from the given point is equal to the given line ${\color{#000} \rule[-0.5em]{1cm}{2pt} }$.
Q.E.D.
I made a Geogebra of this proposition: