George Hart’s Card Constructions

George Hart is a sculptor and geometer, and his webpage has the best projects for the artistically-minded nerd!
The image above shows the 30-cards construction, but it is not identical to what George Hart shows on his card constructions page. I actually used Francesco De Comité’s version, also credited by Hart. The idea is that you strategically cut the cards in very specific places, so that they can be slided together.
Figuring out how to cut the cards was quite hard to me, I had to experiment a lot! George Hart provides printable templates, but their dimensions are different from the cards I used. Finally besides cutting the cards, the task of putting everything together was a nightmare. It’s been a while since I built this, but I think that I used clothes pegs to hold the cards together before the whole thing is ready. Once you finish building the structure, it should be much more stable (but not enough to throw it in the air!!).
Because there is a 5-fold symmetry, naturally the golden ratio
\[\varphi = \frac{1+\sqrt{5}}{2}\]
figures quite prominently in there. Francesco De Comité provides in his Flickr page a plan for how to cut the cards:

I put the plan above for the future me to understand what it means, because I myself didn’t use this… I found in one of my “projects” folders my own calculations of how to cut the cards. It shows only the cuts on the top side. One should rotate the card 180 degrees and do the same cuts on the other side. For a card of height H and length L, my cutting plan is the following.
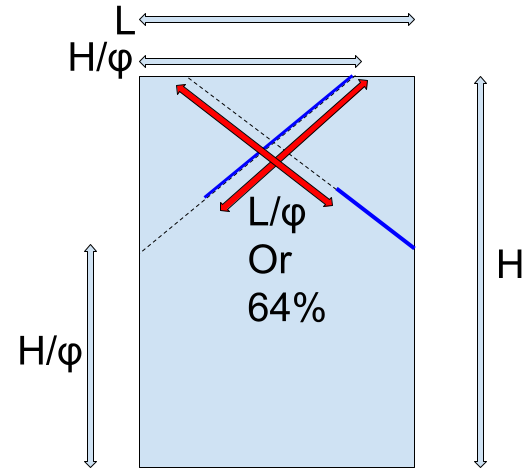
The cuts are the thick blue lines, and the red arrows show the length \(L/\varphi\) of one of the cuts and of the uncut (dashed) part. From this I hope you can imagine that when the cards are slided together, the two cuts amount to the length of the whole “diagonal”, such that the two card ends are flush. I wish I could explain why the plan is what it is, but some time has passed and I have no idea any more 🤷♂️…
